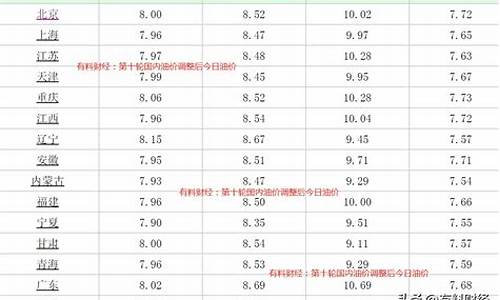
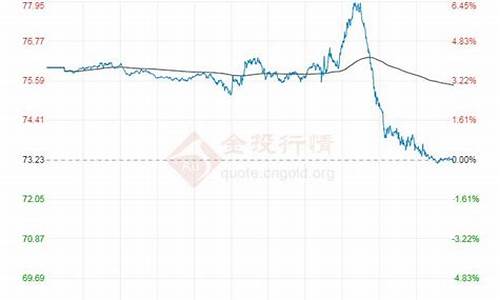
油价涨价怎么算_油价算法永远涨价了吗是真的吗

1.求百公里油耗算法： 比如40升油跑了500公里 合百公里油耗多少 求算法

1.为什么油箱容积都不准

《汽车燃油箱安全性能要求和试验方法》规定:汽车燃油箱的额定容量应控制在燃油箱最大安全容量的95%。也就是说，如果你的车配置表上写着油箱容积为60L,那么实际容积则是63L(有的甚至更大)，多出那3L是国家和汽车厂商出于安全考虑，给油箱留出的余量。

2.油表指针真的准确吗?

大部分汽车油表是用浮子的方式带动油表指针显示油箱存油量，仅通过液面高度来判断油量，自然是不准确的。虽然有的厂商会根据油箱形状，通过算法调整油表指针来做修正，但即便如此，液面计油的方式仍然是不准确滴，一般都会有些误差。

3.加油频繁跳枪咋回事?

简单来说，就是油液淹没进气嘴，大气压的压差导致开关自动关闭。导致频繁“跳枪”的原因，很有可能是油枪插入的姿势不对，影响到了空气与开关膜上腔之间的连通，导致提前产生气压差，以至于油枪关闭。

4.早上加油能“赚”吗?

正规加油站，汽油柴油存在地下储油罐中，而且这个储油罐还有多层的防腐套装，基本上和地面温度做到了隔绝，早晚温差对地下储油罐的影响微乎其微。也就是说，你加满一个油箱，也就“赚”了不到1块钱。而且你还免不了要把油箱撑满吧?

5.雷雨天最好不加油

在雷雨天气状态下加油，加油枪极易将电流导入汽车油箱，从而造成不稳定汽油的分子运动加剧，从而引发火灾、爆炸等安全隐患。而在加油站中，燃油蒸汽浓度相比于其他地方明显要高出很多，如果还继续进行加油操作，燃油蒸汽容易被雷击中，导致车辆和油罐发生爆炸。

6.发现油罐车先不加油

如果你正准备进站加油，发现油槽上停着一部油罐车，这个时候请调转车头继续找下一家加油站。因为油罐车补充的油料，会涌起槽底多年的沉积，很有可能就加到你的油箱里。如果这些杂质进入到发动机缸内，会影响发动机使用寿命。

7.一次不要加得太满

为油箱加油，最好控制在安全容积内，油枪自动跳枪时应停止加油，给油箱留有一定的安全挥发空间。如果汽油加到油箱口部，多余汽油会进入汽油蒸发系统管路，造成混合气过浓，这样会对发动机造成损坏。

8.标号越高越好吗?

车主只需按照车辆使用手册建议的标号去加油即可，不能随便降低标号，但是也不需要自己人为地使用高标号。92和95其实只是油气的标号，代表的是抗爆性，化学术语叫做汽油的辛烷值，它真心与清洁度没有关系，适合的才是最好的。

求百公里油耗算法： 比如40升油跑了500公里 合百公里油耗多少 求算法

队列是一种先进先出的数据结构，由于这一规则的限制，使得队列有区别于栈等别的数据结构。

作为一种常用的数据结构，同栈一样，是有着丰富的现实背景的。以下是几个典型的例子。

[例5-2] 一个旅行家想驾驶汽车以最少的费用从一个城市到另一个城市(设出发时油箱是空的).给定两个城市之间的距离D1,汽车油箱的容量C(以升为单位),每升汽油能行驶的距离D2,出发点每升汽油价格P和沿途油站数N(N可以为零),油站i离出发点的距离Di,每升汽油价格Pi(i=1,2,……N).

计算结果四舍五入至小数点后两位.

如果无法到达目的地,则输出"No Solution".

样例:

INPUT

D1=275.6 C=11.9 D2=27.4 P=2.8 N=2

油站号I

离出发点的距离Di

每升汽油价格Pi

1

102.0

2.9

2

220.0

2.2

OUTPUT

26.95(该数据表示最小费用)

[问题分析]

看到这道题,许多人都马上判断出穷举是不可行的,因为数据都是以实数的形式给出的.但是,不用穷举,有什么方法是更好的呢 递推是另一条常见的思路,但是具体方法不甚明朗.

既然没有现成的思路可循,那么先分析一下问题不失为一个好办法.由于汽车是由始向终单向开的,我们最大的麻烦就是无法预知汽车以后对汽油的需求及油价变动;换句话说,前面所买的多余的油只有开到后面才会被发觉.

提出问题是解决的开始.为了着手解决遇到的困难,取得最优方案,那就必须做到两点,即只为用过的汽油付钱;并且只买最便宜的油.如果在以后的行程中发现先前的某些油是不必要的,或是买贵了,我们就会说:"还不如当初不买."由这一个想法,我们可以得到某种启示:设我们在每个站都买了足够多的油,然后在行程中逐步发现哪些油是不必要的,以此修改我们先前的购买,节省资金;进一步说,如果把在各个站加上的油标记为不同的类别,我们只要在用时用那些最便宜的油并为它们付钱,其余的油要么是太贵,要么是多余的,在最终的中会被排除.要注意的是,这里的便宜是对于某一段路程而言的,而不是全程.

[算法设计]由此,我们得到如下算法:从起点起(包括起点),每到一个站都把油箱加满(终点除外);每经过两站之间的距离,都按照从便宜到贵的顺序使用油箱中的油,并计算花费,因为这是在最优方案下不得不用的油;如果当前站的油价低于油箱中仍保存的油价,则说明以前的购买是不够明智的,其效果一定不如购买当前加油站的油,所以,明智的选择是用本站的油代替以前购买的高价油,留待以后使用,由于我们不是真的开车,也没有为备用的油付过钱,因而这样的反悔是可行的;当我们开到终点时,意味着路上的费用已经得到,此时剩余的油就没有用了,可以忽略.

数据结构用一个队列:存放由便宜到贵的各种油,一个头指针指向当前应当使用的油(最便宜的油),尾指针指向当前可能被替换的油(最贵的油).在一路用一路补充的过程中同步修改数据,求得最优方案.

注意:每到一站都要将油加满,以确保在有解的情况下能走完全程.并设出发前油箱里装满了比出发点贵的油,将出发点也看成一站,则程序循环执行换油,用油的操作,直到到达终点站为止.

本题的一个难点在于认识到油箱中油的可更换性,在这里,突破现实生活中的思维模式显得十分重要.

[程序清单]

program ex5_2(input,output);

const max=1000;

type recordtype=record price,content:real end;

var i,j,n,point,tail:longint;

content,change,distance2,money,use:real;

price,distance,consume:array[0..max] of real;

oil:array [0..max] of recordtype;

begin

write('Input DI,C,D2,P:'); readln(distance[0],content,distance2,price[0]);

write('Input N:'); readln(n); distance[n+1]:=distance[0];

for i:=1 to n do

begin

write('Input D[',i,'],','P[',i,']:');

readln(distance[i],price[i])

end;

distance[0]:=0;

for i:=n downto 0 do consume[i]:=(distance[i+1]-distance[i])/distance2;

for i:=0 to n do

if consume[i]>content then

begin writeln('No Solution'); halt end;

money:=0; tail:=1; change:=0;

oil[tail].price:=price[0]*2; oil[tail].content:=content;

for i:=0 to n do

begin

point:=tail;

while (point>=1) and (oil[point].price>=price[i]) do

begin

change:=change+oil[point].content;

point:=point-1

end;

tail:=point+1;

oil[tail].price:=price[i];

oil[tail].content:=change;

use:=consume[i]; point:=1;

while (use>1e-6) and (point=oil[point].content

then begin use:=use-oil[point].content;

money:=money+oil[point].content*oil[point].price;

point:=point+1 end

else begin oil[point].content:=oil[point].content-use;

money:=money+use*oil[point].price;

use:=0 end;

for j:=point to tail do oil[j-point+1]:=oil[j];

tail:=tail-point+1;

change:=consume[i]

end;

writeln(money:0:2)

end.

[例5-3] 分油问题:设有大小不等的3个无刻度的油桶,分别能够存满,X,Y,Z公升油(例如X=80,Y=50,Z=30).初始时,第一个油桶盛满油,第二,三个油桶为空.编程寻找一种最少步骤的分油方式,在某一个油桶上分出targ升油(例如targ=40).若找到解,则将分油方法打印出来;否则打印信息"UNABLE"等字样,表示问题无解.

[问题分析] 这是一个利用队列方法解决分油问题的程序.分油过程中,由于油桶上没有刻度,只能将油桶倒满或者倒空.三个油桶盛满油的总量始终等于开始时的第一个油桶盛满的油量.

[算法设计] 分油程序的算法主要是,每次判断当前油桶是不是可以倒出油,以及其他某个油桶是不是可以倒进油.如果满足以上条件,那么当前油桶的油或全部倒出,或将另一油桶倒满,针对两种不同的情况作不同的处理.

程序中使用一个队列Q,记录每次分油时各个油桶的盛油量和倾倒轨迹有关信息,队列中只记录互不相同的盛油状态(各个油桶的盛油量),如果程序列举出倒油过程的所有不同的盛油状态,经考察全部状态后,未能分出TARG升油的情况,就确定这个倒油问题无解.队列Q通过指针front和rear实现倒油过程的控制.

[程序清单]

program ex5_3(input,output);

const maxn=5000;

type stationtype=array[1..3] of integer;

elementtype=record

station:stationtype;

out,into:1..3;

father:integer

end;

queuetype=array [1..maxn] of elementtype;

var current,born:elementtype;

q:queuetype;

full,w,w1:stationtype;

i,j,k,remain,targ,front,rear:integer;

found:boolean;

procedure addQ(var Q:queuetype;var rear:integer; n:integer; x:elementtype);

begin

if rear=n

then begin writeln('Queue full!'); halt end

else begin rear:=rear+1; Q[rear]:=x end

end;

procedure deleteQ(var Q:queuetype;var front:integer;rear,n:integer;var x:elementtype);

begin

if front=rear

then begin writeln('Queue empty!'); halt end

else begin front:=front+1; x:=Q[front] end

end;

function dup(w:stationtype;rear:integer):boolean;

var i:integer;

begin

i:=1;

while (i<=rear) and ((w[1]q[i].station[1]) or

(w[2]q[i].station[2]) or (w[3]q[i].station[3])) do i:=i+1;

if i0 then

begin

print(q[k].father);

if k>1 then write(q[k].out, ' TO ',q[k].into,' ')

else write(' ':8);

for i:=1 to 3 do write(q[k].station[i]:5);

writeln

end

end;

begin {Main program}

writeln('1: ','2: ','3: ','targ');

readln(full[1],full[2],full[3],targ);

found:=false;

front:=0; rear:=1;

q[1].station[1]:=full[1];

q[1].station[2]:=0;

q[1].station[3]:=0;

q[1].father:=0;

while (front begin

deleteQ(q,front,rear,maxn,current);

w:=current.station;

for i:=1 to 3 do

for j:=1 to 3 do

if (ij) and (w[i]>0) and (w[j]remain

then begin w1[j]:=full[j]; w1[i]:=w[i]-remain end

else begin w1[i]:=0; w1[j]:=w[j]+w[i] end;

if not(dup(w1,rear)) then

begin

born.station:=w1;

born.out:=i;

born.into:=j;

born.father:=front;

addQ(q,rear,maxn,born);

for k:=1 to 3 do

if w1[k]=targ then found:=true

end

end

end;

if not(found)

then writeln('Unable!')

else print(rear)

end.

40升油跑了500公里合百公里油耗为8L，具体计算方法如下：

40L÷500km=8L/km，如当日93#油价为6.5元，折合人民为=8L/kmx6.5元/100=0.52元/km。

油耗的测量方法：

可以到固定加油站，在同样的加油站用同样的加油枪把油加到跳枪或慢慢的加到刚刚流出时后，把里程表归零，可以专门跑一趟100公里或长途，也可以就是实际上下班使用的里程，跑到附油箱加油告急灯亮时，再到同样的加油站用同样的加油枪把油加到跳枪或慢慢的加到刚刚流出时计算加进多少油。用加的油和跑的公里数计算出百公里的油耗。

扩展资料：

权威的油耗测试

在专门的实验车场的专门跑道上，在规定的湿度、气压、胎压等，在满载等速的条件下（秤重坐满人和后背箱加配重物）；用专门的计量仪器（带刻度的量杯、流量计等）切断车辆原来的供油系统，用计量仪器量杯内的油跑几十或百米（好象是这样的，不计算加速时的油耗，不能滑行）的来回路后，除二计算出的百公里等油耗等的数据。

比较准确的油耗测试

由专门的人选择实验的路，用专门的带刻度的油箱跑100公里的来回路后（可以计算进加速时的油耗，但是不能滑行），除二计算出的实际百公里等油耗的数据。

百度百科-油耗